“That which is provable, ought not to be believed in science without proof,” said Richard Dedekind. The formula for the volume of a pyramid is usually learnt in junior forms without any proof. One may think that such proofs require calculus. In fact the formula was well known before the invention of calculus. If we look back to the history, we can find some explanations and proofs which are comprehensible to lower form students. These proofs are more accessible with the use of the dynamic GeoGebra 3D figures.
The following approach of deriving the formula for volume of a pyramid was reported to be originated from Democritus (Edwards 1979, p.8-10). In the first figure below, a red triangular pyramid is “completed” to form a prism together with the blue and the green pyramids. Check each of the boxes and drag the blue slider, we can see that the red and the blue pyramids, and also the blue and the green pyramids, always have equal sections at equal heights (the 2nd and the 3rd figures below). Considering that a pyramid is composed of sections parallel to its base, the red pyramid and the blue pyramid are then equal in volumes, and so are the blue and the green pyramids (Cavalieri’s principle). Since the three pyramids composing the prism are equal in volumes, the volume of the red pyramid is therefore one-third of that of the prism, and hence one-third of its base area times the height.
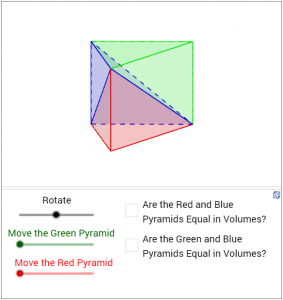
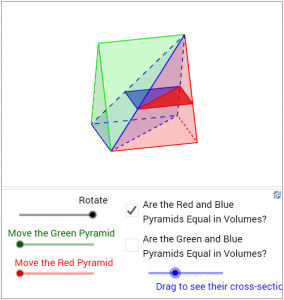
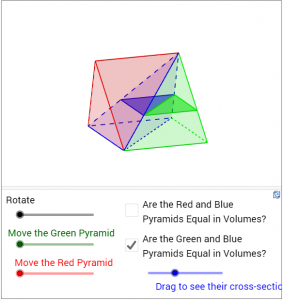
(Click here to access the dynamic figure.)
It is worthwhile to note that a Chinese mathematician LIU Hui (劉徽, fl. 3rd century) proved the result in an ingenious way. In his commentary of the Chinese’s mathematical classics “Arithmetic in Nine Chapters (九章算術)”, the triangular prism is divided into a triangular pyramid and a rectangular pyramid (the 1st figure below). After pressing the “Start” and then the “Next” button, with the midpoints of the edges each of the pyramids are divided into some prisms (the red and yellow parts) and some empty smaller pyramids. It is clear that the sum of the volumes of the red parts is half of that of the yellow parts (the 2nd figure below).
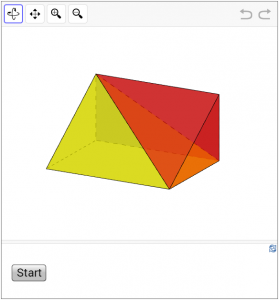
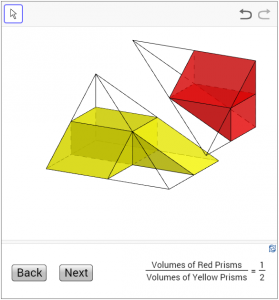
(Click here to access the dynamic figure.)
The smaller pyramids can be further divided up accordingly (press the “Next” button again to see). Again the sum of the volumes of the red parts is half of that of the yellow parts. The same process can be continued indefinitely (press the “Next” button repeatedly) and we shall see that the limiting shapes, the red triangular pyramid and the yellow rectangular pyramid, have the ratio 1 : 2 in volumes. Therefore the volume of the red triangular pyramid is one-third of that of the prism, and hence the result.
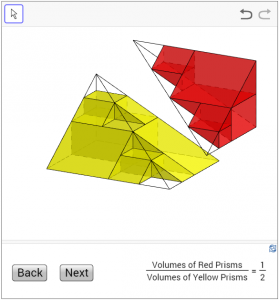
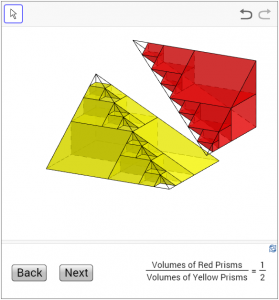
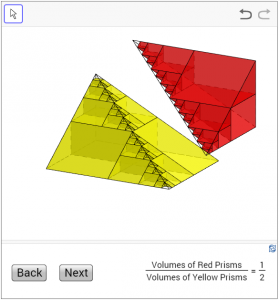

(Click here to access the dynamic figure.)
LIU Hui expressed his idea of carrying the process to the limit as follows (Wagner, 1979):
The smaller they are halved, the finer are the remaining. The extreme of the fineness is called “subtle”. That which is subtle is without form. When it is explained in this way, why concern oneself with the remainder?
It is particularly impressive that LIU Hui could visualize this subtle limit process, as illustrated by the above dynamic figure, without the help of modern technology.
The above two applets are also available in the GeoGebraBook: http://tube.geogebra.org/material/show/id/359361.
References
Edwards, C. H. Jr. 1979. The Historical Development of the Calculus. Springer-Verlag, New York
Wagner, D.B. 1979. An Early Chinese Derivation of the Volume of a Pyramid: Liu Hui, Third Century A.D. Historia Mathematica 6 p.164-188


















