In the post “Volume of Pyramids with GeoGebra” some elementary proofs of the formula for the volume of a pyramid illustrated with GeoGebra are introduced. In this post, some methods of deriving the formula for the volume of spheres would be presented with the use of GeoGebra.
Eves (1990) presents a proof of the formula as follows. In the figure,
 (Click the figure for the GeoGebra applet)
(Click the figure for the GeoGebra applet)
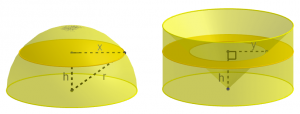
the area of the cross-section of the hemisphere
![]()
the area of the cross-section of the solid at the RHS
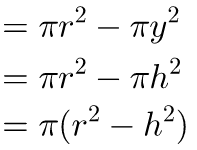
Hence the areas of the cross-sections of the two solids at the same height are always equal. By Cavalieri’s principle the volumes of two solids are equal. Hence the volume of the sphere
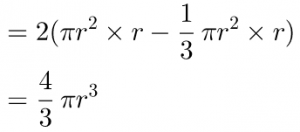
Ancient Chinese mathematicians approached the problem in a different way. In the classic problem book the Nine Chapters on the Mathematical Art, the volume of a sphere was incorrectly given as π²d³/16 (d = diameter). Chinese mathematician LIU Hui (劉徽, fl. 3rd century) explained the error as follows. It is known that the ratio of the area of a circle inscribed in a square to the area of the square is π/4. So the ratio of the volume of a cylinder inscribed in a cube to the volume of the cube is also π/4, because each cross-section is a circle inscribed in the square and the ratio of their areas is always π/4.

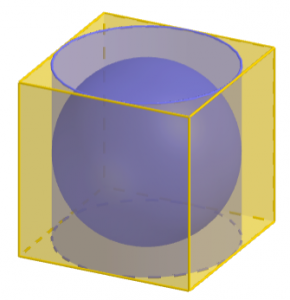

(Click the figure for the GeoGebra applet.)
Now consider also the sphere inscribed in the cube. If we assume, incorrectly, that the ratio of the volume of the sphere to the volume of the cylinder is also π/4, then we would get the volume of the sphere is π²d³/16.
LIU Hui pointed out that the object whose volume is 4/π times that of the sphere should be obtained by replacing each of its cross-section by the circumscribing square (see the figure). He called this object a “double box-lid” (Mouhefanggai 蓋合方蓋). He also pointed out that this object is the intersection of two orthogonal cylinder of the same radius (see the figure).


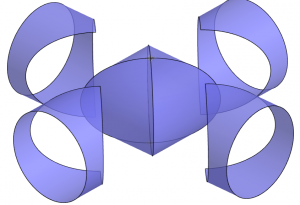 (Click the figure for the GeoGebra applet.)
(Click the figure for the GeoGebra applet.)
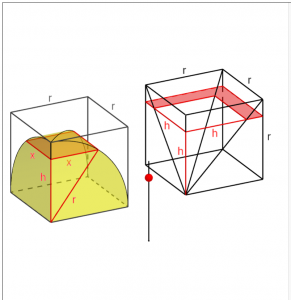
LIU Hui was unable to find the volume of the double box-lid. The problem was only solved two centuries later by ZU Gengzhi (祖暅之), the son of the famous mathematician ZU Chongzhi (祖沖之). As shown in the figure below, ZU Gengzhi showed that the volume of the difference between an octant of the double box-lid and the cube containing it is equal to the volume of a pyramid whose volume is one-third of that of the cube. Hence the volume of the double box-lid, and also the volume of the sphere, were found.
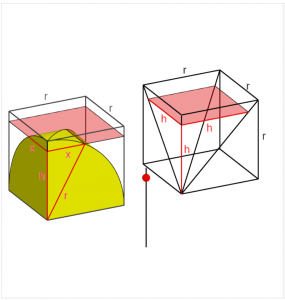
 (Click the figure for the GeoGebra applet.)
(Click the figure for the GeoGebra applet.)
If we try to look at the area of the cross-section of the octant of the double box-lid directly, we could show that its volume is two-third of that of the cube, as shown in the following figures.

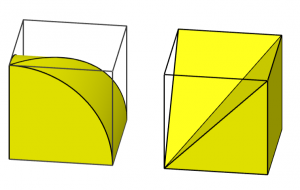
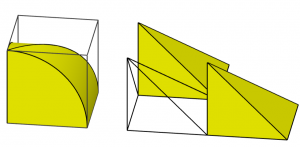 (Click the figure for the GeoGebra applet.)
(Click the figure for the GeoGebra applet.)
Final Remark
It is hoped that the GeoGebra applets presented in these two posts on volumes of pyramids and spheres could help teachers to bridge the “logical gaps” (Tzanakis and Arcavi 2000 p.204-207) in the introduction of these formulas to lower form students without proofs. These materials are also valuable to provide problems to motivate and engage students in the teaching and learning of the formulas.
References
Eves, H. 1990. An introduction to the history of mathematics (Sixth Ed.). Saunders College Publishing
Tzanakis, C., Arcavi, A. 2000. ‘Integrating history of mathematics in the classroom: an analytic survey’, in J. Fauvel and J. van Maanen (eds.), History in Mathematics Education, Kluwer Academic Publishers, 201 – 240
Wagner, D . B. (1978) ‘Liu Hui and Tsu Keng-chih on the volume of a sphere’, Chinese Science Vol.3, 59-79






Thanks Anthony for your effort in preparing this and sharing it with all of us! Great article
Thanks, Vincent!
Youtube, I really don't like the new layout, it was fine how it was before. You keep making changes that no one asks for and many people complain about them. With every change you have made over the past year, I have been able to use Youtube less effectively than I had before the change. If you want to make a new home page, fine, do it, but don't force it on us, let us choose which one we want to use, the old one or the new one.
: type in e-bandhana in your youtube search bar. you wont get the exact song. but a version of it. it’s pretty nice man. i love it too despite being a non kannadiga.
Hello Nice wewebsite. Do you need to invitee submit in my own someday? If so make sure you tell me by way of e mail or just answer this particular remark simply due to the fact My partner and my spouse and i actually subscribed to notifications and can know should you choose.
As will trumpeting the killer's name, picture, and "motive".I suspect that Cerebrus' fire sale bath will be less than they'd lose from all the institutional investor pullouts.
I’m still outraged and seething on your behalf too.This woman has no respect for children … one wonders how she tackles the whole issue of God and religion!I would send a letter to the school but also send a copy of it to your Local Education Authority representative and your local MP. State that it’s not just about the incident now but also about how the school have handled (or not handled) your compaint. Oh. And if nobody takes a blind bit of notice, contact your local paper too.
I have to give kudos the the One Million Moms. Really. It appears that they've finally learned how to use vowels again.sex – well down OMM! I applaud you.
GeoGebra is my favorite mathematical software. Thank You for great article.
Good morning!
I’m a unfledged one here. and I have occasion for a brief notice about writing my homewrk. I’ve right-minded found the perfect article with opportunity to get homework help online that is satiated of academic expos tipsHow do you think, can it be worthwhile for my college research?
Have a nice day!
Clark