In the post “Volume of Pyramids with GeoGebra” some elementary proofs of the formula for the volume of a pyramid illustrated with GeoGebra are introduced. In this post, some methods of deriving the formula for the volume of spheres would be presented with the use of GeoGebra.
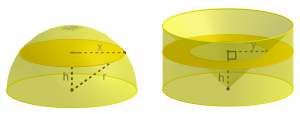
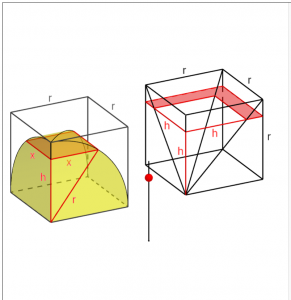
Eves (1990) presents a proof of the formula as follows. In the figure,
(Click the figure for the GeoGebra applet)
the area of the cross-section of the hemisphere
the area of the cross-section of the solid at the RHS
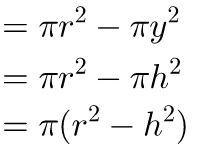
Hence the areas of the cross-sections of the two solids at the same height are always equal. By Cavalieri’s principle the volumes of two solids are equal. Hence the volume of the sphere
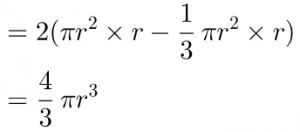
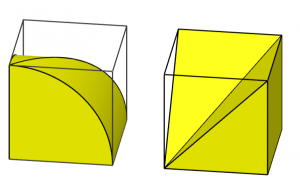
Ancient Chinese mathematicians approached the problem in a different way. In the classic problem book the Nine Chapters on the Mathematical Art, the volume of a sphere was incorrectly given as π²d³/16 (d = diameter). Chinese mathematician LIU Hui (劉徽, fl. 3rd century) explained the error as follows. It is known that the ratio of the area of a circle inscribed in a square to the area of the square is π/4. So the ratio of the volume of a cylinder inscribed in a cube to the volume of the cube is also π/4, because each cross-section is a circle inscribed in the square and the ratio of their areas is always π/4.
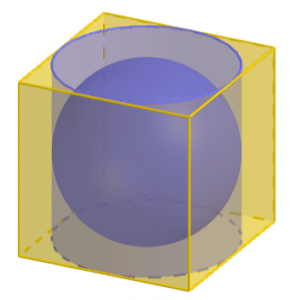
(Click the figure for the GeoGebra applet.)
Now consider also the sphere inscribed in the cube. If we assume, incorrectly, that the ratio of the volume of the sphere to the volume of the cylinder is also π/4, then we would get the volume of the sphere is π²d³/16.
LIU Hui pointed out that the object whose volume is 4/π times that of the sphere should be obtained by replacing each of its cross-section by the circumscribing square (see the figure). He called this object a “double box-lid” (Mouhefanggai 蓋合方蓋). He also pointed out that this object is the intersection of two orthogonal cylinder of the same radius (see the figure).
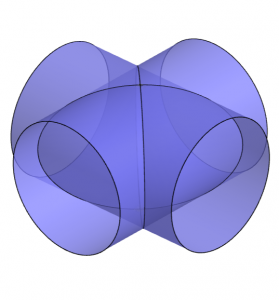
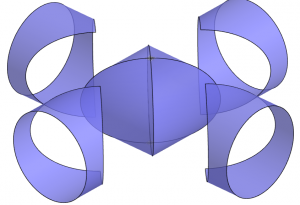(Click the figure for the GeoGebra applet.)
LIU Hui was unable to find the volume of the double box-lid. The problem was only solved two centuries later by ZU Gengzhi (祖暅之), the son of the famous mathematician ZU Chongzhi (祖沖之). As shown in the figure below, ZU Gengzhi showed that the volume of the difference between an octant of the double box-lid and the cube containing it is equal to the volume of a pyramid whose volume is one-third of that of the cube. Hence the volume of the double box-lid, and also the volume of the sphere, were found.
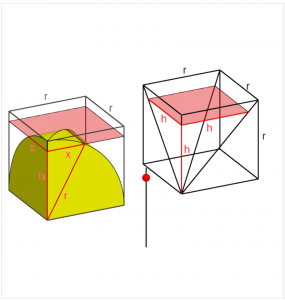
(Click the figure for the GeoGebra applet.)
If we try to look at the area of the cross-section of the octant of the double box-lid directly, we could show that its volume is two-third of that of the cube, as shown in the following figures.
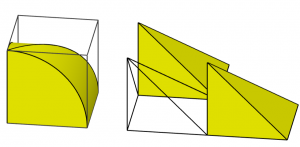(Click the figure for the GeoGebra applet.)
Final Remark
It is hoped that the GeoGebra applets presented in these two posts on volumes of pyramids and spheres could help teachers to bridge the “logical gaps” (Tzanakis and Arcavi 2000 p.204-207) in the introduction of these formulas to lower form students without proofs. These materials are also valuable to provide problems to motivate and engage students in the teaching and learning of the formulas.
References
Eves, H. 1990. An introduction to the history of mathematics (Sixth Ed.). Saunders College Publishing
Tzanakis, C., Arcavi, A. 2000. ‘Integrating history of mathematics in the classroom: an analytic survey’, in J. Fauvel and J. van Maanen (eds.), History in Mathematics Education, Kluwer Academic Publishers, 201 – 240
Wagner, D . B. (1978) ‘Liu Hui and Tsu Keng-chih on the volume of a sphere’, Chinese Science Vol.3, 59-79
→ Forum 
